数学:関数とグラフ
一次関数のグラフ
一次関数のグラフを書く汎用的なプログラムを示します。傾きや切片を書き換えて、様々な一次関数のシミュレーション表示を簡単に行うことができます。
教員が授業で利用したり、生徒が演習や予復習で利用することができます。
PCはもちろん、Chromebook, iPAD,スマートフォンなどでも、PyTermなどを使用してプログラムを実行してグラフを表示させることができます。
import matplotlib.pyplot as plt
a, b = 1, 2 # 傾きと切片
xs, xe = -5, 9 # 定義域:xの下限と上限
def f(x): # 関数の定義
return a*x + b # 一次関数:直線
x = list(range(xs,xe+1))
y = [f(i) for i in x]
# print("x: ", x) # xの内容確認
# print("y: ", y) # yの内容確認
plt.clf() # グラフの設定の初期化
ax=plt.subplot()
ax.set_title('Linear Function') # グラフタイトルの設定
ax.set_aspect('equal') # XY軸の目盛りの縦横比を1に
ax.spines['bottom'].set_position('zero') # 下部のX軸目盛りをy=0の場所に移動
ax.spines['left'].set_position('zero') # 左のY軸目盛りをx=0の場所に移動
ax.spines['top'].set_visible(False) # 上部の枠を消す
ax.spines['right'].set_visible(False) # 右の枠を消す
ax.tick_params(direction='inout')
ys = min(y)-1 if min(y) < 0 else -2 # Y軸の表示範囲にX軸y=0が含まれるように計算
ye = max(y)+1 if max(y) > 0 else 2
ax.set_ylim(ys, xe) # Y軸の表示範囲を指定
plt.xticks(x)
plt.yticks(range(int(ys), int(ye)+1))
plt.grid(visible=True) #
title = f'y={a if a!=1 else ""}x{b:+d}' # タイトルの作成
plt.plot(x,y, label=title) # データのプロット
ax.legend() # 凡例を表示
plt.show()- 3行目のa, bに傾きと切片を指定します。
- 4行目のxs, xeに定義域を指定します。
3,4行目の設定を変えるだけで、このプログラムを使用して、様々な一次関数グラフを簡単に表示させることができます。
プログラムをそのまま実行すると、以下のようなグラフが表示されます。
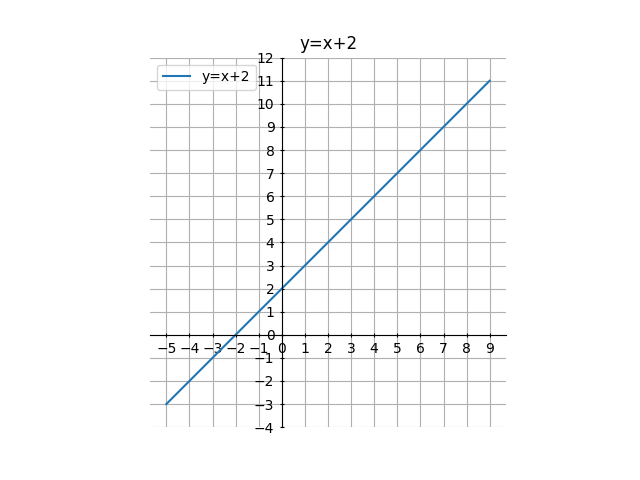
例えば、3行目の傾きと切片を-1, 15に設定して再度プログラムを実行すると、以下のようなグラフが表示されます。
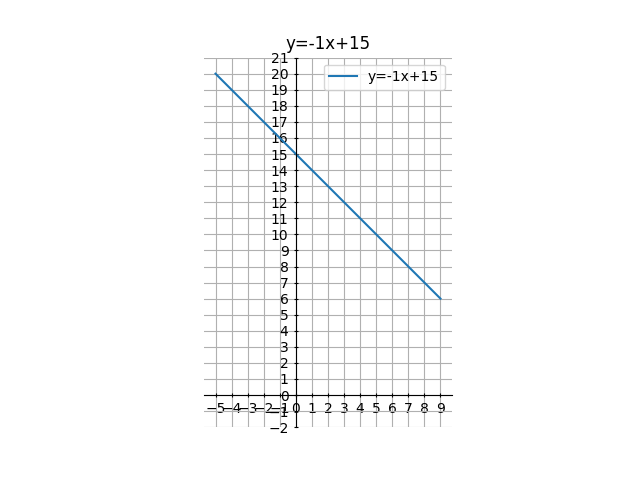
この例では、直線の値域の下限が正になっていますが、原点とⅹ軸の目盛りがグラフに含まれるように、グラフの表示領域が調整されています。
このように3, 4行目の設定を変えて、様々な一次関数のグラフを簡単に表示させることができます。
プログラムの15行に以下の指示が書かれていますが、これをコメントアウトして傾きと切片を書き換えてプログラムを繰り返し実行すると、複数の関数グラフを一つの図に重ね書きすることができます。
plt.clf()例えば、以下のような3種類の設定でプログラムを3回実行させると以下のようなグラフが表示されます。
- a, b = 1, 2
- a, b = -1, 15
- a, b = 1, 10
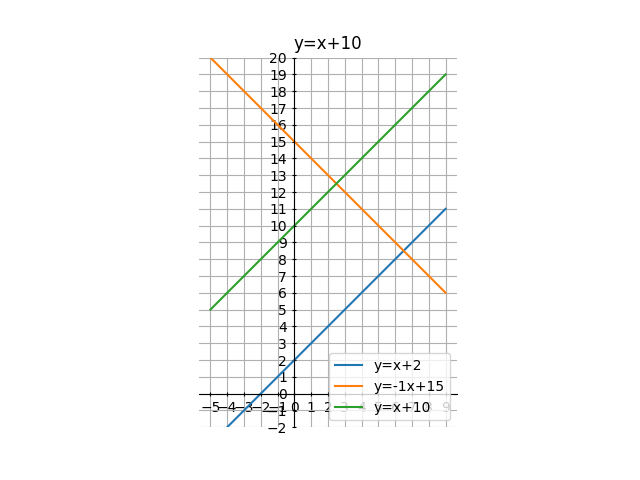
グラフ表示プログラムの作成過程
まず、matplotlibを使用して一次関数のグラフを書く基本的なプログラムを書いてみましょう。
出発点となるプログラムの処理手順は以下の通り。
- ライブラリをインポートする
- 傾きと切片、定義域を定義する
- (数学的な)関数を(プログラムの)関数として定義する
- グラフとしてプロットするx,y値を収めるための空のリストを作成する
- 定義域の下限から上限まで1間隔で以下の処理を繰り返す
- x, y=f(x)の値をx, yのリストに追加する
- リストx,yの値を確認のため表示する
- グラフ表示の初期化をする
- グラフの格子の表示を指定
- x, y リストの内容をグラフに描画
- グラフの図を表示する
上記の処理手順を元に書いたPythonのプログラムを以下に示します。
import matplotlib.pyplot as plt
a = 1 # 傾き
b = 2 # 切片
xs = -5 # 定義域:xの下限と上限
xe = 9
def f(x): # 関数の定義
return a*x + b # 一次関数:直線
x = []
y = []
for i in range(xs, xe+1):
x.append(i)
y.append(f(i))
print("x: ", x) # xの内容確認
print("y: ", y) # yの内容確認
plt.clf()
plt.grid(visible=True)
plt.plot(x,y)
plt.show()このプログラムを実行すると、以下のようなグラフが表示されます。
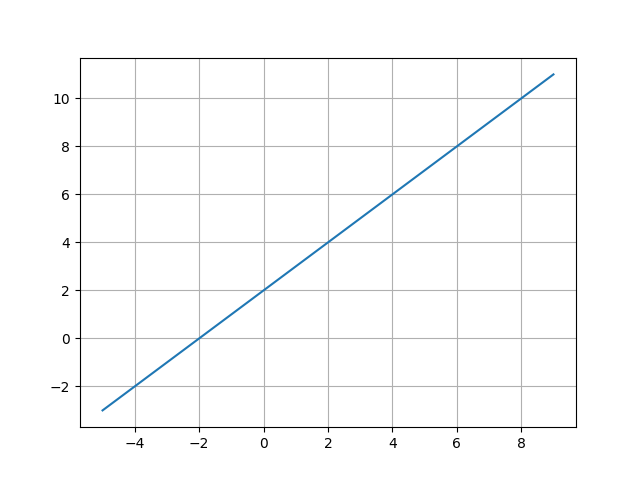
これはこれで綺麗ですが、シンプルなグラフが表示されました。用途に寄りますが、以下のような問題や不足がありそうです。
- 縦軸と横軸の間隔が異なっており、グラフの正しい形が分からない。
- 原点を通るX軸、Y軸が書かれていない。
- 定義域や地域がどのようになっても、原点が表示されるようにしたい。
- 複数のグラフを重ねて書くのであれば、凡例が欲しい。
これら問題や不足を解決していきましょう。
一次関数:Xの値の生成法を変更
xのリストをまず作り、xのリストから対応するyのリストを作る
import matplotlib.pyplot as plt
a = 1 # 傾き
b = 2 # 切片
xs = -5 # 定義域:xの下限と上限
xe = 9
def f(x): # 関数の定義
return a*x + b # 一次関数:直線
x = list(range(-5,10))
print("x: ", x) # xの内容確認
y = []
for i in x:
y.append(f(i))
print("y: ", y) # yの内容確認
plt.clf()
plt.grid(visible=True)
plt.plot(x,y)
plt.show()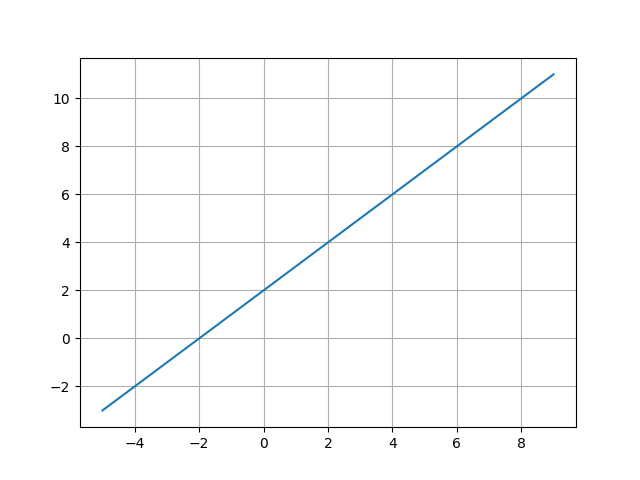
import matplotlib.pyplot as plt
a, b = 1, 2 # 傾きと切片
xs, xe = -5, 9 # 定義域:xの下限と上限
def fx(x): # 関数の定義
return a*x + b # 一次関数:直線
x = list(range(xs,xe+1))
#y = []
#for i in x:
# y.append(fx(i))
y = [fx(i) for i in x]
print("x: ", x) # xの内容確認
print("y: ", y) # yの内容確認
plt.clf()
ax=plt.subplot()
ax.set_title(f'y={a if a!=1 else ""}x{b:+d}') # グラフタイトルの設定
ax.set_aspect('equal') # 縦横比を1に
ax.spines['bottom'].set_position('zero') # 下部のX軸目盛りをy=0の場所に移動
ax.spines['left'].set_position('zero') # 左のY軸目盛りをx=0の場所に移動
ax.spines['top'].set_visible(False) # 上部の枠を消す
ax.spines['right'].set_visible(False) # 右の枠を消す
ax.tick_params(direction='inout')
ys = min(y)-1 if min(y) < 0 else -2
ye = max(y)+1 if max(y) > 0 else 2
ax.set_ylim(ys, xe)
plt.xticks(x)
plt.yticks(range(int(ys), int(ye)+1))
plt.grid(visible=True) #
plt.plot(x,y) # データのプロット
plt.show()二次関数
import matplotlib.pyplot as plt
a = 1 #
b = 2 #
c = 3 #
def fx(x):
return a*x**2 + b*x + c # 二次曲線
x = list(range(-2,2))
print("x: ", x) # xの内容確認
y = []
for i in x:
y.append(fx(i))
print("y: ", y) # yの内容確認
plt.clf()
ax=plt.subplot()
ax.set_title(f'y={a:}x^2{b:+d}x{c:+d}')
ax.set_aspect('equal')
ax.set_xlim(-2,1)
ax.set_ylim(-1,7)
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.tick_params(direction='inout')
plt.subplot().set_aspect('equal')
plt.grid(visible=True)
plt.plot(x,y)
plt.show()import matplotlib.pyplot as plt
a = 1 #
b = 2 #
c = 3 #
def fx(x):
return a*x**2 + b*x + c # 二次曲線
x = list(range(-2,2))
print("x: ", x) # xの内容確認
y = []
for i in x:
y.append(fx(i))
print("y: ", y) # yの内容確認
plt.clf()
plt.grid(visible=True)
plt.plot(x,y)
plt.show()import matplotlib.pyplot as plt
a = 1 #
b = 2 #
c = 3 #
def fx(x):
return a*x**2 + b*x + c # 二次曲線
x = list(range(-2,2))
print("x: ", x) # xの内容確認
y = []
for i in x:
y.append(fx(i))
print("y: ", y) # yの内容確認
plt.clf()
ax=plt.subplot()
ax.set_title(f'y={a:}x^2{b:+d}x{c:+d}')
ax.set_aspect('equal')
ax.set_xlim(-2,1)
ax.set_ylim(-1,7)
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.tick_params(direction='inout')
plt.subplot().set_aspect('equal')
plt.grid(visible=True)
plt.plot(x,y)
plt.show()import matplotlib.pyplot as plt
a = 1 # 傾き
b = 2 # 切片
def fx(x):
return a*x + b # 直線
x = list(range(-5,10))
print("x: ", x) # xの内容確認
y = []
for i in x:
y.append(fx(i))
print("y: ", y) # yの内容確認
plt.clf()
ax=plt.subplot()
ax.set_title('y='+str(a)+'x+'+str(b))
ax.set_aspect('equal')
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.tick_params(direction='inout')
plt.grid(visible=True)
plt.plot(x,y)
plt.show()import matplotlib.pyplot as plt
a = 1 #
b = 2 #
c = 3 #
def fx(x):
return a*x**2 + b*x + c # 二次曲線
x = list(range(-2,2))
print("x: ", x) # xの内容確認
y = []
for i in x:
y.append(fx(i))
print("y: ", y) # yの内容確認
plt.clf()
plt.grid(visible=True)
plt.plot(x,y)
plt.show()