このページの内容は文科省の以下の資料を基に作成されたものです。
- 高等学校情報科「情報Ⅰ」教員研修用教材(本編)
確定モデルと確率モデル
複利計算
yokin = 100000 # 預金
riritsu = 0.05 # 利率
for i in range(10): #i の値を 0 から 9 まで 10 回繰り返す
risoku = yokin*riritsu # その年の利息
yokin = yokin + risoku # 預金に利息を加える
print(i+1," 年目 :",yokin) # 画面に表示複利計算結果のグラフ表示
import matplotlib.pyplot as plt # プロットオブジェクトをインポート
riritsu = 0.05 # 利率
yokin = [100000] # 預金配列の最初の値は 10 万
for i in range(10): #i の値を 0 〜 9 まで、10 回繰り返す
risoku = int(yokin[i]*riritsu) # 利息は現在の預金額 × 利率 ( 整数化 )
yokin.append(yokin[i]+risoku) # 配列に計算結果を追加
plt.title("FUKURI KEISAN") # グラフのタイトル
plt.xlabel("Year") #X 軸のラベル
plt.ylabel("Yokin[YEN]") #Y 軸のラベル
plt.plot(yokin, marker="o") # グラフをプロット
plt.show()サンプルプログラムは入試に出ないリストを使用。
リストを使用しているがリストを配列とみなして使用をした例を以下に示す。
import matplotlib.pyplot as plt # プロットオブジェクトをインポート
gankin = 100000 # 元金
riritsu = 0.05 # 利率
year = 10 # 10年
yokin = [0]*(year+1) # 初年度と10年の11要素のリスト(配列)を初期化
yokin[0] = gankin # 初年度の頭金を設定
for i in range(year): #i の値を 0 〜 9 まで、10 回繰り返す
risoku = yokin[i]*riritsu # 利息は現在の預金額 × 利率 ( 整数化 )
yokin[i+1] = yokin[i]+risoku # 配列に計算結果を代入
plt.title("FUKURI KEISAN") # グラフのタイトル
plt.xlabel("Year") #X 軸のラベル
plt.ylabel("Yokin[YEN]") #Y 軸のラベル
plt.plot(yokin, marker="o") # グラフをプロット
plt.show()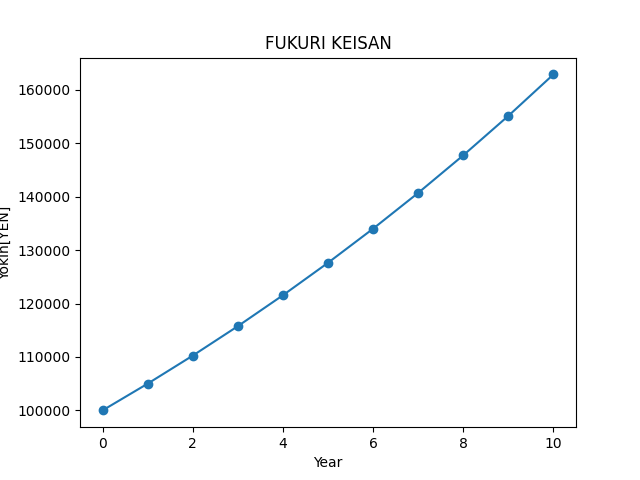
乱数発生
import numpy.random as rd # 乱数を発生させる関数の呼び出し
ransuu = rd.rand() #0 〜 1 の乱数を 1 個生成
print(" 乱数 ", ransuu) # 乱数の値を表示サイコロ
import numpy as np # 整数をカウントするための関数呼び出し
import numpy.random as rd # 乱数を発生させる関数の呼び出し
saikoro = rd.randint(1, 6+1, 100) # サイコロを 100 回振る
print(saikoro) # 乱数の値を表示
deme = [ ] # 出目の数を数える配列
for i in range(6):
deme.append(np.count_nonzero(saikoro==i+1)) # 出現回数を数えて配列に追加
print(" 出現数 :",deme) # 乱数の値を表示サンプルプログラムは入試に出ないリストを使用。
リストを使用しているがリストを配列とみなして使用をした例を以下に示す。
import numpy as np # 整数をカウントするための関数呼び出し
import numpy.random as rd # 乱数を発生させる関数の呼び出し
me = 6
saikoro = rd.randint(1, me+1, 100) # サイコロを 100 回振る
print(saikoro) # 乱数の値を表示
deme = [0]*me # 出目の数を数える配列
for i in range(me):
deme[i] = np.count_nonzero(saikoro==i+1) # 出現回数を数えて配列に追加
print(" 出現数 :",deme) # 乱数の値を表示サイコロの度数分布
import numpy as np # 整数をカウントするための関数呼び出し
import numpy.random as rd # 乱数を発生させる関数の呼び出し
import matplotlib.pyplot as plt # グラフプロットの呼び出し
saikoro = rd.randint(1, 6+1, 100) # サイコロを 100 回振る
deme = [ ] # 出目の数を数える配列
for i in range(6):
deme.append(np.count_nonzero(saikoro==i+1)) # 数を数えて配列に追加
left = [1, 2, 3, 4, 5, 6] # グラフの左方向の値指定用
plt.title("SAIKORO SIMULATION") # グラフのタイトル
plt.xlabel("ME") #X 軸のラベル
plt.ylabel("KAISUU") #Y 軸のラベル
plt.bar(left, deme, align="center") # グラフをプロット
plt.show() # プロットオブジェクトを表示サンプルプログラムは入試に出ないリストを使用。
リストを使用しているがリストを配列とみなして使用をした例を以下に示す。
import numpy as np # 整数をカウントするための関数呼び出し
import numpy.random as rd # 乱数を発生させる関数の呼び出し
import matplotlib.pyplot as plt # グラフプロットの呼び出し
me = 6
saikoro = rd.randint(1, me+1, 100) # サイコロを 100 回振る
print(saikoro) # 乱数の値を表示
deme = [0]*me # 出目の数を数える配列
for i in range(me):
deme[i] = np.count_nonzero(saikoro==i+1) # 出現回数を数えて配列に追加
left = [1, 2, 3, 4, 5, 6] # グラフの左方向の値指定用
plt.title("SAIKORO SIMULATION") # グラフのタイトル
plt.xlabel("ME") #X 軸のラベル
plt.ylabel("KAISUU") #Y 軸のラベル
plt.bar(left, deme, align="center") # グラフをプロット
plt.show()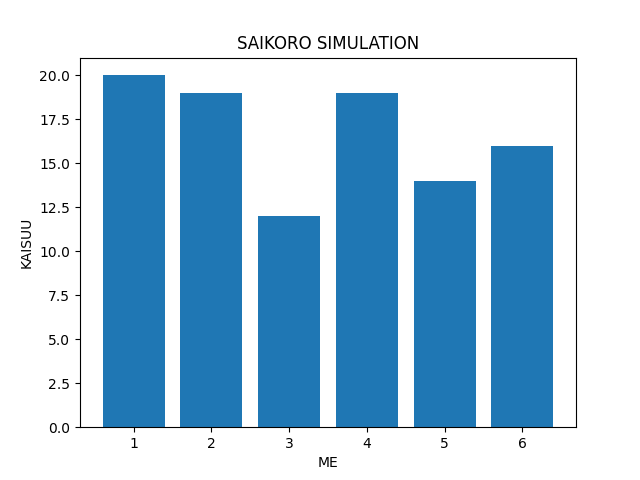
モンテカルロ法による円周率
import numpy.random as rd # 乱数を発生させる関数の呼び出し
totalcount = 1000 # ランダムに打つ点の総数
incount = 0 # 円に入った点の数
for i in range(totalcount):
x = rd.random() #0-1 の範囲の値
y = rd.random() #0-1 の範囲の値
if x**2 + y**2 < 1.0: # 単位円の中に入ったら
incount += 1 # 入ったカウンターに1を加える
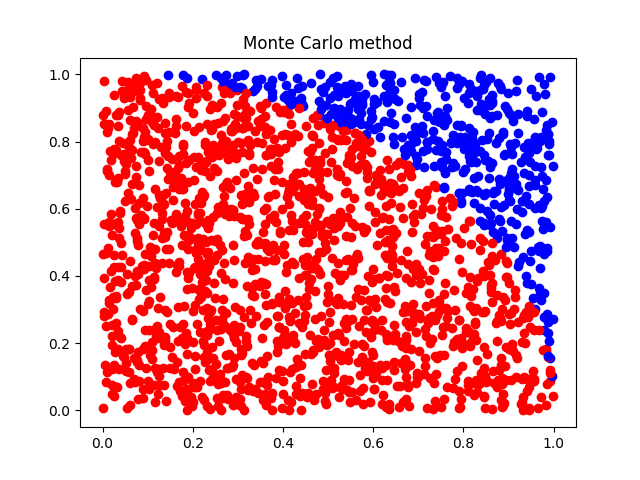
print(" 円周率 :", incount * 4.0 / totalcount) # 求まった円周率モンテカルロ法の散布図
import numpy.random as rd # 乱数を発生させる関数の呼び出し
import matplotlib.pyplot as plt # グラフプロットの呼び出し
totalcount = 2000 # ランダムに打つ点の総数
incount = 0 # 円に入った点の数
for i in range(totalcount):
x = rd.random() #0-1 の範囲の値
y = rd.random() #0-1 の範囲の値
if x**2 + y**2 < 1.0: # 単位円の中に入ったら
incount += 1 # 入ったカウンターに1を加える
plt.scatter(x, y, c="red") # 赤色でプロット
else:
plt.scatter(x, y, c="blue") # 青色でプロット
print(" 円周率 :", incount * 4.0 / totalcount) # 求まった円周率
plt.title("Monte Carlo method") # グラフのタイトル
plt.show()