このページの内容は文科省の以下の資料を基に作成されたものです。
- 高等学校情報科「情報Ⅰ」教員研修用教材(本編)
自然現象のモデル化とシミュレーション
物体の放物運動
import math as math # 数値計算ライブラリ
import matplotlib.pyplot as plt # グラフ描画ライブラリ
dt = 0.01 # 微小時間 ( 時間間隔 )
v0 = 30 # 初速度
g = 9.8 # 重力加速度
x = [0] # 水平位置の初期値 0
y = [0] # 鉛直位置の初期値は 0
angle = 45.0 * math.pi / 180.0 # 投げ上げ角度
vx = [v0*math.cos(angle)] # 水平方向の初速度
vy = [v0*math.sin(angle)] # 鉛直方向の初速度
for i in range(1000):
vx.append(vx[i]) # 微小時間後の水平方向の速度
vy.append(vy[i]-g*dt) # 微小時間後の鉛直方向の速度
x.append(x[i]+vx[i]*dt) # 微小時間後の水平位置
y.append(y[i]+(vy[i]+vy[i+1])/2.0*dt) # 微小時間後の鉛直位置
if y[i] < 0 : # もし鉛直位置が 0 を下回ったら
break # ループ中断
plt.plot(x,y) # 位置の配列をプロット
plt.title("parabollic motion") # グラフのタイトル
plt.xlabel("distance") #x 軸ラベル
plt.ylabel("height") #y 軸ラベル
plt.show()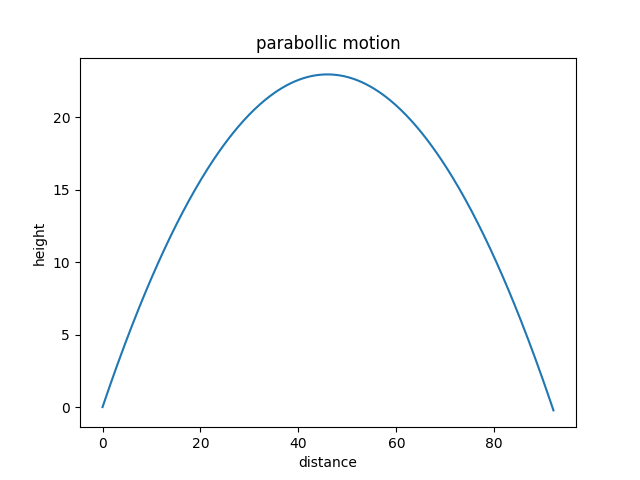
生命体の増加シミュレーション
元資料のリスト(の要素追加機能)使用版
少なくともこれまでの共通テストの試行問題ではリストの使用は考慮されていないので、この方法のみの学習では共通テストでは解答できない。
import matplotlib.pyplot as plt # グラフ描画ライブラリ
zouka = 0.01 # 増加率
capacity = 1000 # 環境収容数
n = [10] # 最初の個体数
for i in range(1000):
zoukasuu = n[i]*zouka # 増加数
gensyousuu = n[i]*(n[i]/capacity)*zouka # 減少数
n.append(n[i]+(zoukasuu - gensyousuu)) # 個体数
plt.plot(n) # グラフにプロット
plt.title("number of life") # グラフのタイトル
plt.xlabel("time") #x 軸のラベル
plt.ylabel("number") #y 軸のラベル
plt.show()リストを(疑似)配列として使用した版
import matplotlib.pyplot as plt # グラフ描画ライブラリ
zouka = 0.01 # 増加率
capacity = 1000 # 環境収容数
trials = 1000 # 試行回数(世代数)
n = [0]*(trials+1) # 個体数を記録する配列を作成
n[0] = 10 # 最初の個体数
for i in range(trials):
zoukasuu = n[i]*zouka # 増加数
gensyousuu = n[i]*(n[i]/capacity)*zouka # 減少数
n[i+1] = n[i]+(zoukasuu - gensyousuu) # 個体数
plt.plot(n) # グラフにプロット
plt.title("number of life") # グラフのタイトル
plt.xlabel("time") #x 軸のラベル
plt.ylabel("number") #y 軸のラベル
plt.show()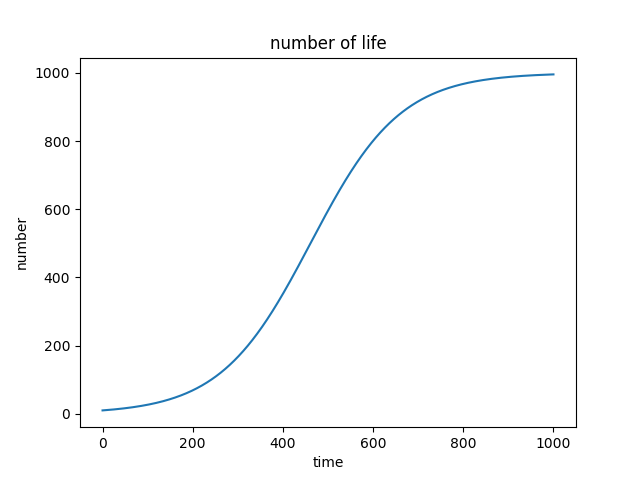
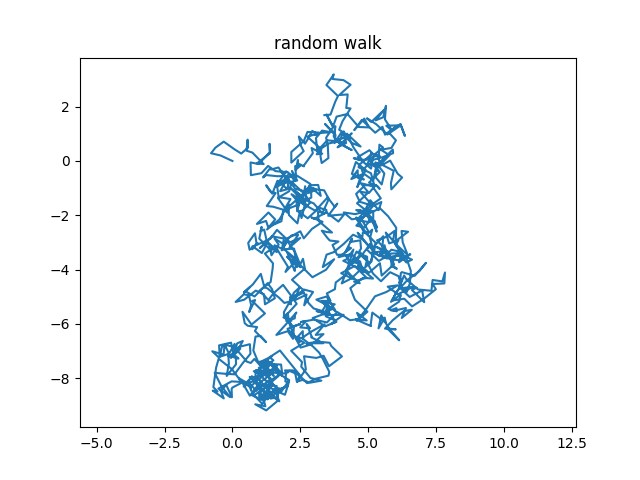
ランダムウォーク
元資料のリスト(の要素追加機能)使用版
少なくともこれまでの共通テストの試行問題ではリストの使用は考慮されていないので、この方法のみの学習では共通テストでは解答できない。
import matplotlib.pyplot as plt # グラフ描画ライブラリ
import numpy.random as rd # 乱数のためのライブラリ
trials = 1000 # 試行回数
x=[0] # X の初期値を 0 にする
y=[0] # Y の初期値を 0 にする
for i in range(trials):
x.append(x[i]+rd.random() - 0.5) # X 方向
y.append(y[i]+rd.random() - 0.5) # Y 方向
plt.plot(x, y) # 配列要素のグラフ描画
plt.axis("equal") # グラフの縦横比を等しく
plt.title("random walk") # グラフのタイトルをつける
plt.show() # グラフを表示リストを(疑似)配列として使用した版
import matplotlib.pyplot as plt # グラフ描画ライブラリ
import numpy.random as rd # 乱数のためのライブラリ
trials = 1000 # 試行回数
x=[0]*(trials+1) # 初期値0と、試行回数分の座標値を記録できる配列を作る
y=[0]*(trials+1)
for i in range(trials):
x[i+1] = (x[i]+rd.random() - 0.5) #X 方向
y[i+1] = (y[i]+rd.random() - 0.5) #Y 方向
plt.plot(x,y) # 配列要素のグラフ描画
plt.axis("equal") # グラフの縦横比を等しく
plt.title("random walk") # グラフのタイトルをつける
plt.show() # グラフを表示